- Klikova: 6566
Njutnov zadatak o domaćim životinjama

Izložit ćemo Njutnov problem o domaćim životinjama i kratku anegdotu o Njutnu i njegovim mačkama. Ovom slavnom matematičaru i fizičaru se pripisuje pronalazak otvora sa poklopcem na ulaznim vratima za kućne ljubimce. Njutn je, naime, imao dvije mačke, jednu malu i drugu veliku. Da bi omogućio svojim mačkama da izlaze i ulaze kad god žele a da ga pritom ne uznemiravaju u radu, on je napravio dva otvora: jedan mali za malu mačku i drugi veći za veliku mačku. U svojoj rasijanosti nije se sjetio da mu je veći otvor dovoljan za obje mačke.
Mada je Njutn rješavao uglavnom teže i izazovne probleme koji leže u osnovama moderne matematike, neki od njih mogu se uvrstiti u zadatke rekreativne matematike. Tipičan primjer je zadatak koji navodimo preuzet iz Njutnove knjige Arithmetica universalis (Opšta aritmetika).
akra (stara engleska mjera za površinu i iznosi 40,468 ari ili 4046,8 m2 ) za 4 nedelje, i ako 21 vo popase 10 akra pašnjaka za 9 nedelja, koliko volova će pojesti svu travu sa pašnjaka površine 24 akra za 18 nedelja. Napomenimo da trava neprestano raste jednakom brzinom svakog dana.
Notice: Trying to get property 'id' of non-object in /home/matemati/public_html/templates/shaper_helix3/html/com_content/category/blog_item.php on line 72
- Klikova: 32907
Kvadratura kruga
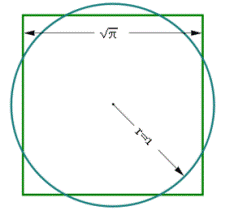 Kvadratura kruga je jedan od najstarijih i najpoznatijih matematičkih problema:
Kvadratura kruga je jedan od najstarijih i najpoznatijih matematičkih problema:
Konstruisati kvadrat
čija je površina jednaka
površini datog kruga.
- Klikova: 6593
Zadatak sa kvadratima
Notice: Trying to get property 'id' of non-object in /home/matemati/public_html/templates/shaper_helix3/html/com_content/category/blog_item.php on line 72
- Klikova: 19082
Udvostručavanje kocke
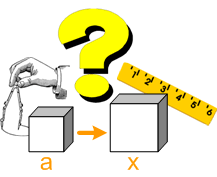 Tri osnovna klasična geometrijska problema su:
Tri osnovna klasična geometrijska problema su:
- udvostručavanje kocke;
- kvadratura kruga;
- trisekcija ugla.
Do konačnog odgovora na ova pitanja čekalo se više od dvije hiljade godina. Problem udvostručavanja kocke sastoji se u tome da se prema zadanoj kocki konstruiše kocka dvostruko veće zapremine.
- Klikova: 25293
Trisekcija ugla
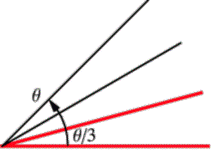 Problem trisekcije ugla su nametnule stvarne potrebe, Grci su svoje hramove i mnoge spomenike ukrašavali raznim ornamentima čija je konstrukcija zahtjevala dijeljenje ugla na tri podudarna ugla.
Problem trisekcije ugla su nametnule stvarne potrebe, Grci su svoje hramove i mnoge spomenike ukrašavali raznim ornamentima čija je konstrukcija zahtjevala dijeljenje ugla na tri podudarna ugla.
Ovaj zadatak potiče još od Hipije (4. vijek p.n.e.), a sastoji se u tome da se zadani ugao elementarnom geometrijskom konstrukcijom podijeli na tri jednaka dijela. Poznato je da se ugao može podijeliti na 2n podudarnih uglova, gdje je n prirodan broj. Ovaj postupak su pronašli Grci. Oni su znali za trisekciju nekih uglova.
- Klikova: 5615
Novac u rukama
 Robert Recorde (oko 1510 - 1558), jedan od najutjecajnijih engleskih pisaca udžbenika 16. vijeka, bio je ljekar, matematičar i astronom. U svojoj knjizi "The Whetstone of Witte" (1557.) uveo je moderni simbol za jednakost "=". Mada je radio kao ljekar na dvoru kralja Edvarda VI i kraljice Meri i kasnije postao kontrolor rudnika novca u Irskoj, Robert je bio uhapšen pod misterioznim okolnostima i umro je u zatvoru 1558. godine. Sljedeći zadatak objavljen je u njegovoj knjizi:
Robert Recorde (oko 1510 - 1558), jedan od najutjecajnijih engleskih pisaca udžbenika 16. vijeka, bio je ljekar, matematičar i astronom. U svojoj knjizi "The Whetstone of Witte" (1557.) uveo je moderni simbol za jednakost "=". Mada je radio kao ljekar na dvoru kralja Edvarda VI i kraljice Meri i kasnije postao kontrolor rudnika novca u Irskoj, Robert je bio uhapšen pod misterioznim okolnostima i umro je u zatvoru 1558. godine. Sljedeći zadatak objavljen je u njegovoj knjizi:
- Neki čovjek ima u obje ruke 8 kruna. Ova suma novca, zajedna sa kvadratima i kubovima svota u svakoj ruci, daje 194. Koliko novaca u svakoj ruci ima čovjek?
Notice: Trying to get property 'id' of non-object in /home/matemati/public_html/templates/shaper_helix3/html/com_content/category/blog_item.php on line 72
