 Tri osnovna klasična geometrijska problema su:
Tri osnovna klasična geometrijska problema su:
- udvostručavanje kocke;
- kvadratura kruga;
- trisekcija ugla.
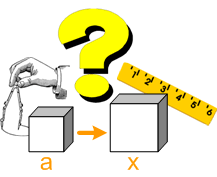
Do konačnog odgovora na ova pitanja čekalo se više od dvije hiljade godina. Problem udvostručavanja kocke sastoji se u tome da se prema zadanoj kocki konstruiše kocka dvostruko veće zapremine.
O rješavanju ovog problema postoji nekoliko legendi. Prema jednoj o njih kralju Ptolemeju II se spomenik njegovog sina, koji je bio sagrađen u obliku kocke, učinio odviše mali te je zatražio da se udvostruči. Graditelji su smatrali da se to može jednostavno riješiti tako što se se ivica postojećeg spomenika udvostručiti, što naravno, nije tačno.
Ako sa a označimo dužinu ivice date kocke, a sa x dužinu ivice kocke čija je zapremina dvaput veća od zapremine date kocke, onda je:
x3 = 2a3
odakle je
x = a 3√2 .
Dakle, potrebno je konstruisati (lenjirom i šestarom) duž koja je 3√2 puta veća od duži dužine a. Na taj način stereometrijski problem je sveden na planimetrijski. Međutim, 3√2 se ne može kontruisati samo lenjirom i šestarom, za razliku od, recimo, broja 2 . Kako su Grci sve probleme rješavali geometrijski, to su i ovaj pokušali riješiti na isti način: lenjirom i šestarom. Poslije niza neuspješnih pokušaja uvidjeli su da je to nemoguće izvesti na elementaran način.
Grci su ovaj problem pokušali riješiti pomoću krivih drugog reda. Tako je Menehmo (oko 350. g. p.n.e.) dao dva rješenja: jedno pomoću dvije parabole, a drugo pomoću parabole i hiperbole. Platon je za rješenje ovog problema koristio krivu trećeg reda. Udvostručavanjem kocke bavili su se i Apolonije (265-170 p.n.e.), Heron (1. vijek), arapski matematičar Al Mahani (rođen 820.), Dekart, Njutn, Maskeroni (18. vijek) i drugi. Eratosten je konstruisao aparat za grafičko rješavanje ovog problema.


